Suppose that you have launched a new business that manufactures solar-powered lawnmowers. You are planning a mail campaign to bring this revolutionary new product to the attention of prospective buyers. However, since it is a small business, you cannot afford to sponsor coast-to-coast television commercials or to send brochures by mail to more than 100 million U.S. households. Instead, you plan to target the most likely customers – those who are environmentally conscious, have higher than average family incomes, and who live in areas where there are enough water and the sunshine to support lawns and solar power.
Fortunately, lots of data are available to help you define your mailing list. Household incomes are routinely reported to banks and other financial institutions when families apply for mortgages, loans, and credit cards. Personal tastes related to issues like the environment are reflected in behaviors such as magazine subscriptions and credit card purchases. Market research companies collect such data and transform it into information by creating “lifestyle segments” – categories of households that have similar incomes and tastes. Your solar lawnmower company can purchase lifestyle segment information by 5-digit ZIP code, or even by ZIP+4 codes, which designate individual households.
Geographic Information Systems
It is astonishing how valuable information from the millions upon millions of transactions that are recorded every day. The fact that lifestyle information products are often delivered by geographic areas, such as ZIP codes, speaks to the appeal of geographic information systems (GIS). The scale of these data and their potential applications are increasing continually with the advent of new mechanisms for sharing information and making purchases that are linked to our GPS-enabled smartphones. A Geographical Information System (GIS) is a computer-based tool used to help people transform geographic data into geographic information.
GIS arose out of the need to perform spatial queries on geographic data (questions addressed to a database such as wanting to know a distance or the location where two objects intersect). A spatial query requires knowledge of locations as well as attributes about that location. For example, an environmental analyst might want to know which public drinking water sources are located within one mile of a known toxic chemical spill. Alternatively, a planner might be called upon to identify property parcels located in areas that are subject to flooding.
Numerous tools exist to help users perform database management operations. Microsoft Excel and Access allow users to retrieve specific records, manipulate the records, and create new user content. ESRI’s ArcGIS allows users to organize and manipulate files, but also map the geographic database files in order to find interesting spatial patterns and processes in graphic form.
Global Positioning Sytems
The use of location-based technologies has reached unprecedented levels. Location- enabled devices, giving us access to a wide variety of LBSs, permeate our households and can be found in almost every mall, office, and vehicle. From digital cameras and mobile phones to in-vehicle navigation units and microchips in our pets, millions of people and countless devices have access to the Global Positioning System (GPS). Most of us have some basic idea of what GPS is, but just what is it, exactly, that we are all connected to?
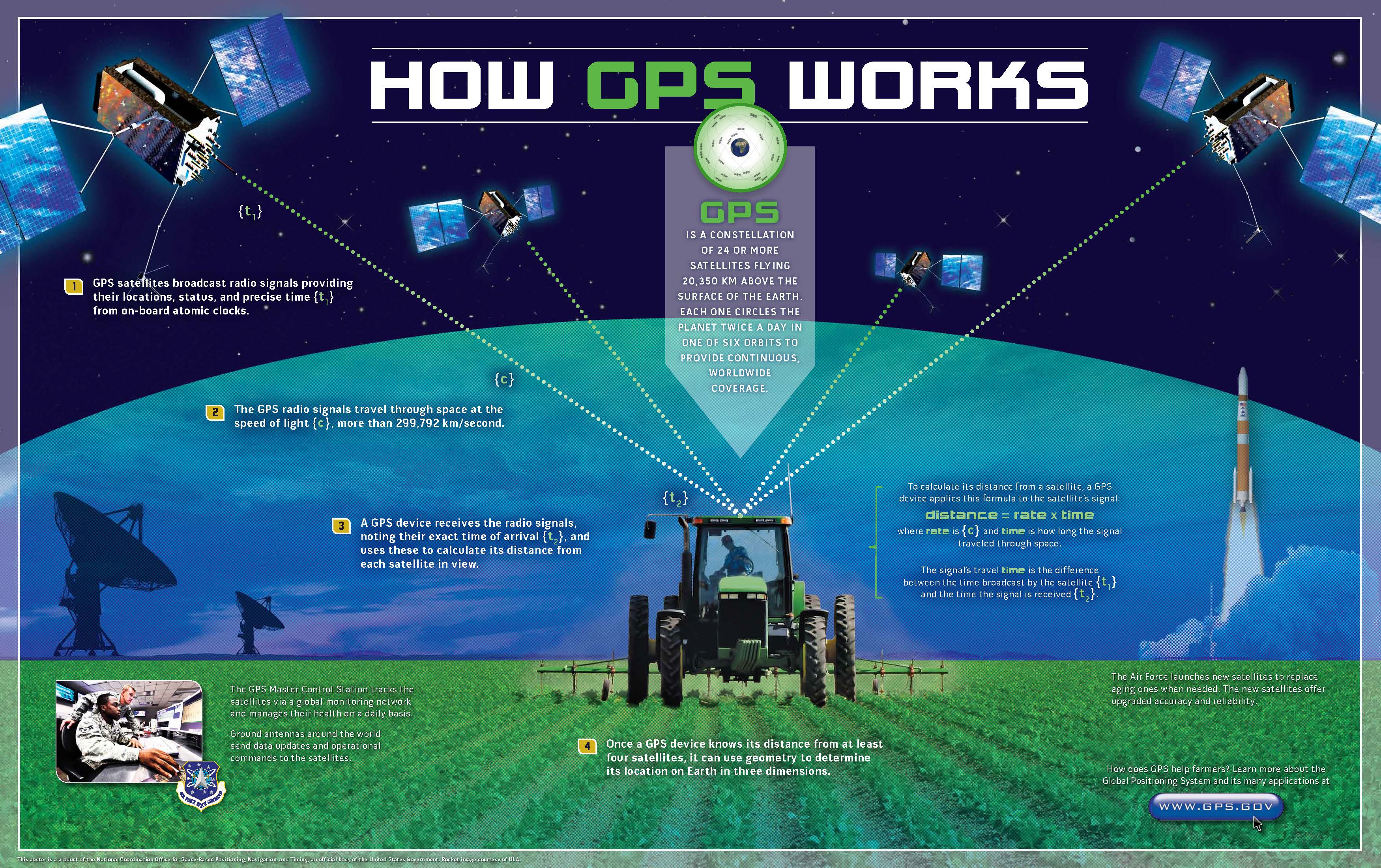
The Global Positioning System (GPS) is a satellite-based navigation system made up of a network of 24 satellites placed into orbit by the U.S. Department of Defense. GPS was originally intended for military applications, but in the 1980s, the government made the system available for civilian use. GPS works in any weather conditions, anywhere in the world, 24 hours a day.
In a nutshell, GPS works like this: satellites circle the Earth twice a day in a very and transmit a signal to Earth. GPS receivers (or smartphones and watches) take this information and use trilateration to calculate the user’s exact location. Now, with distance measurements from a few satellites, the receiver can determine the user’s position and display it on the unit’s electronic map.
Using GPS to determine your location is not very useful if you do not know about the landscape around you. For instance, your GPS could tell you that you are in the mall, but without a map, you may not know how to get to the door. There are many stories of people whose maps were out of date, and they followed their GPS into a river or a lake. Remote sensing allows mapmakers to collect physical data from a distance without visiting or interacting directly with the location.
Remote Sensing
The distance between the object and observer can be considerable, for example, imaging from the Hubble telescope, or rather small, as is the case in the use of microscopes for examining bacterial growth. In geography, the term remote sensing takes on a specific connotation dealing with space-borne and aerial imaging systems used to remotely sense electromagnetic radiation reflected and emitted from Earth’s surface.
Remote sensing systems work in much the same way as a desktop scanner connected to a personal computer. A desktop scanner creates a digital image of a document by recording, pixel by pixel, the intensity of light reflected from the document. Color scanners may have three light sources and three sets of sensors, one each for the blue, green, and red wavelengths of visible light. Remotely sensed data, like the images produced by a desktop scanner, consist of reflectance values arrayed in rows and columns that make up raster grids.
Remote sensing is used to solve a host of problems across a wide variety of disciplines. For example, Landsat imagery is used to monitor plant health and foliar changes. In contrast, imagery such as that produced by IKONOS is used for geospatial intelligence applications (yes, that means spying) and monitoring urban infrastructure. Other satellites, such as AVHRR (Advanced High-Resolution Radiometer), are used to monitor the effects of global warming on vegetation patterns on a global scale. The MODIS (Moderate Resolution Imaging Spectroradiometer) Terra and Aqua sensors are designed to monitor atmospheric and oceanic composition in addition to the typical terrestrial applications.